今天突发奇想,对d20和d100的优势与劣势效果进行了暴力运算,并得出了一个仅供参考的期望数值,计算过程为:
分别对五千次的掷骰优劣势结果进行运算并取平均值,然后重复该过程24次并再取平均值,共计运算十二万次,得出最终的参考期望值。
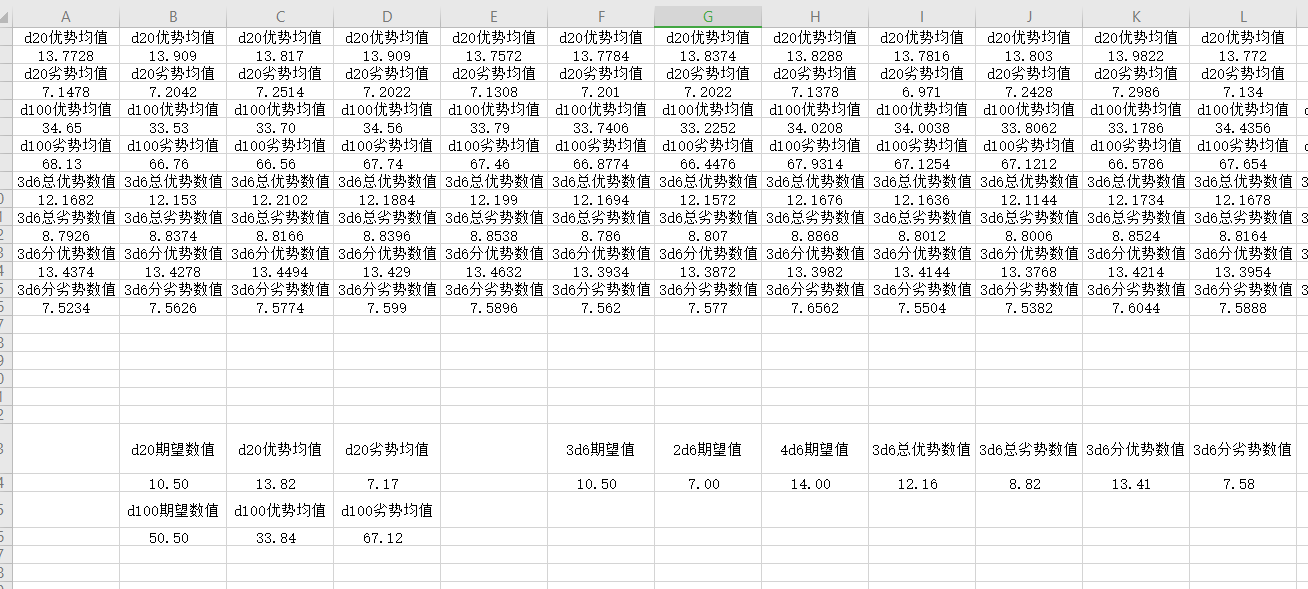
(最后一张图中的3d6优劣势是计算用于朋友基于3d6的原创规则的,总优势为两次3d6之和取高,分优势为两次3d6分别按第一第二第三次的骰值两两取高并合并)
运算结果如下:
d20优势期望值为13.82,劣势期望值为7.17,相较于10.5的期望值,优势相当于+3.3加值,劣势相当于-3.3减值
d100优势期望值为33.84,劣势期望值为67.12,相较于50.5的期望值,优势相当于-16.7的减值,劣势相当于+16.6的加值加上对d2骰优势以及更多其他骰值的计算和分析,大约可以得出“
优劣势会让最终期望值增减最大值的六分之一”的结论,即掷两次取高值会让期望值从50%变为67%,取低值则期望值从50%变为33%。
本人没有玩过COC,因此以下的讨论由DND规则出发。
此运算将优势带来的好处数值化了,可以提供一些优势与加值的取舍建议,我们在下面会对战技大师的“精准攻击”和“诡诈攻击”两个命中技能进行比较。
如果只是单纯的比较数值,“诡诈攻击”的优势所带来的+3.3加值明显是低于“精准攻击”d8战技骰的+4.5期望骰值的,再加之精准攻击骰子可在检定结果出来之后再使用的灵活性,依赖期望值的绝对平均主义者可以很轻松的做出选择。
这里再更进一步的分析优势的细节——大成功与大失败。
DND5E规则中,骰出20则可造成必定命中的重击,造成双倍骰值的伤害,而骰出1则会必定失手,在某些热衷于搞事的村规中,骰出1或20还会有更加不可控的情况发生。在变体规则中更是加入了大成功和大失败的技能检定,让5%的精彩意外变得乐趣纷呈。
而优势则提供了一个额外的能力——将大成功概率从5%提升至9.75%,而大失败概率从5%降低至0.25%,因此我们还要考虑大成功所带来的额外收益的情况。
我们假设这样一个对抗情境:己方攻击骰d20+3,可选使用精准攻击或诡诈攻击,攻击伤害为d9,敌方DC19。
此情境下不使用技能的命中率为25%,命中期望伤害为5,其中有5%的概率触发暴击造成双倍伤害10,则单次攻击造成的伤害期望值为1.5;(这个算法并不十分可靠,仅是作为参考)
若使用精准攻击,则命中率提升至47.5%,命中期望伤害为5,其中有5%的概率触发暴击造成双倍伤害10,则单次攻击造成的伤害期望值为2.625;
若使用诡诈攻击,则命中率提升至41.5%,命中期望伤害为5,其中有10%的概率触发暴击造成双倍伤害10,则单次攻击造成的伤害期望值为2.575,加上诡诈攻击带来的额外伤害加值则为4.8925。
可见在这样一个模拟的对抗高防御敌人的情境下,诡诈攻击可以凭借额外的伤害骰与更高的暴击概率配合实现更高的期望伤害。
上述的例子非常理想化而脱离现实,只能做一个简单的参考,但它仍然可以提示重要的一点:
优势骰的更高暴击几率所带来的双倍伤害概率,是比单纯的命中加值更加立体的。对于无情的至圣斩机器等高伤害骰单位来说,优势骰的收益更是难以想象。
优势骰虽然失去了统计学意义上的常规优势,但是凭借着大成功大失败规则的极端情况所带来的重大收益可能,仍然具备与+4甚至+5加值一较高下的能力,对于那些满心暴击的赌狗玩家来说,可能没有什么比一个优势更香的了。
——什么?你说冠军勇士?哦不,放过我吧...